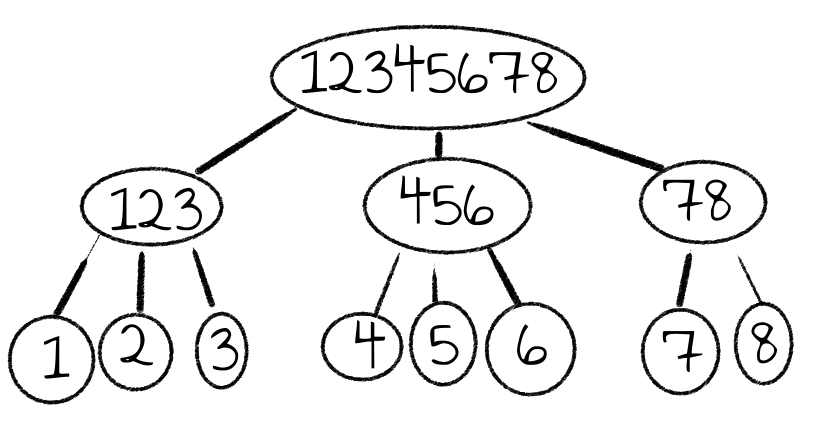
Ternärbäume und Balkenwaagen
In diesem Modul wurden Binärbäume als Modellierungsmethode für Folgen von Ja-Nein-Fragen eingeführt. Auf ähnliche Art und Weise können Ternärbäume – Bäume mit (höchstens) drei Kindern pro Knoten – genutzt werden, um das folgende Rätsel zu lösen:
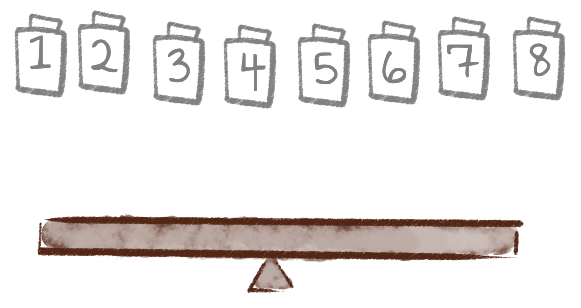
Im Unterricht kann dieses Problem explorativ angegangen werden, indem erst drei Gewichte und ein einziger erlaubter Wiegevorgang betrachtet werden. Hier im Anschluss soll gleich das verallgemeinerte Problem analysiert werden: Gegeben seinen $n$ Gewichte, von denen eines leichter ist. Wie viele Wiegevorgänge werden benötigt, um dieses zu finden?
Die Kerneinsicht zur Lösung des allgemeinen Problems ist, dass bei jedem Wiegevorgang die Gewichte in drei Teilmengen partitioniert werden: Eine für jede Seite der Balkenwaage und eine, die gar nicht gewogen wird.
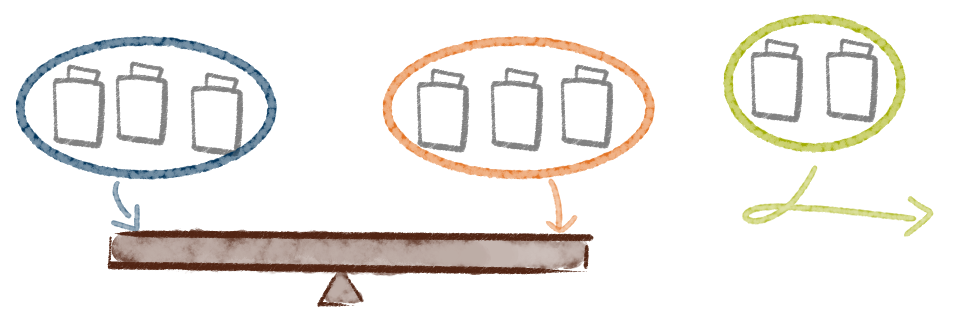
Außerdem hat jeder Wiegevorgang genau eines von drei möglichen Ergebnissen:
- Die Menge auf der linken Seite der Waage ist leichter.
- Die Menge auf der rechten Seite ist leichter.
- Beide Mengen auf der Waage sind gleich schwer.
Und abschließend gibt jedes dieser drei Ergebnisse an, in welcher der drei Mengen das leichtere Gewicht liegt.
- In der linken.
- In der rechten.
- In der, die nicht gewogen wurde.
Damit kann der folgende, rekursive Suchalgorithmus beschrieben werden:
In jedem Schritt wird die Menge an Gewichten, die noch zu analysieren sind, so in drei Mengen A, B und C geteilt,
dass A und B gleich viele Elemente enthalten. Es werden A und B gewogen.
Ist A leichter als B:
Fahre mit A fort.
Ist B leichter als A:
Fahre mit B fort.
Sind beide gleich schwer:
Fahre mit C fort.
Wiederhole den Vorgang, bis nur noch ein Gewicht übrig ist.
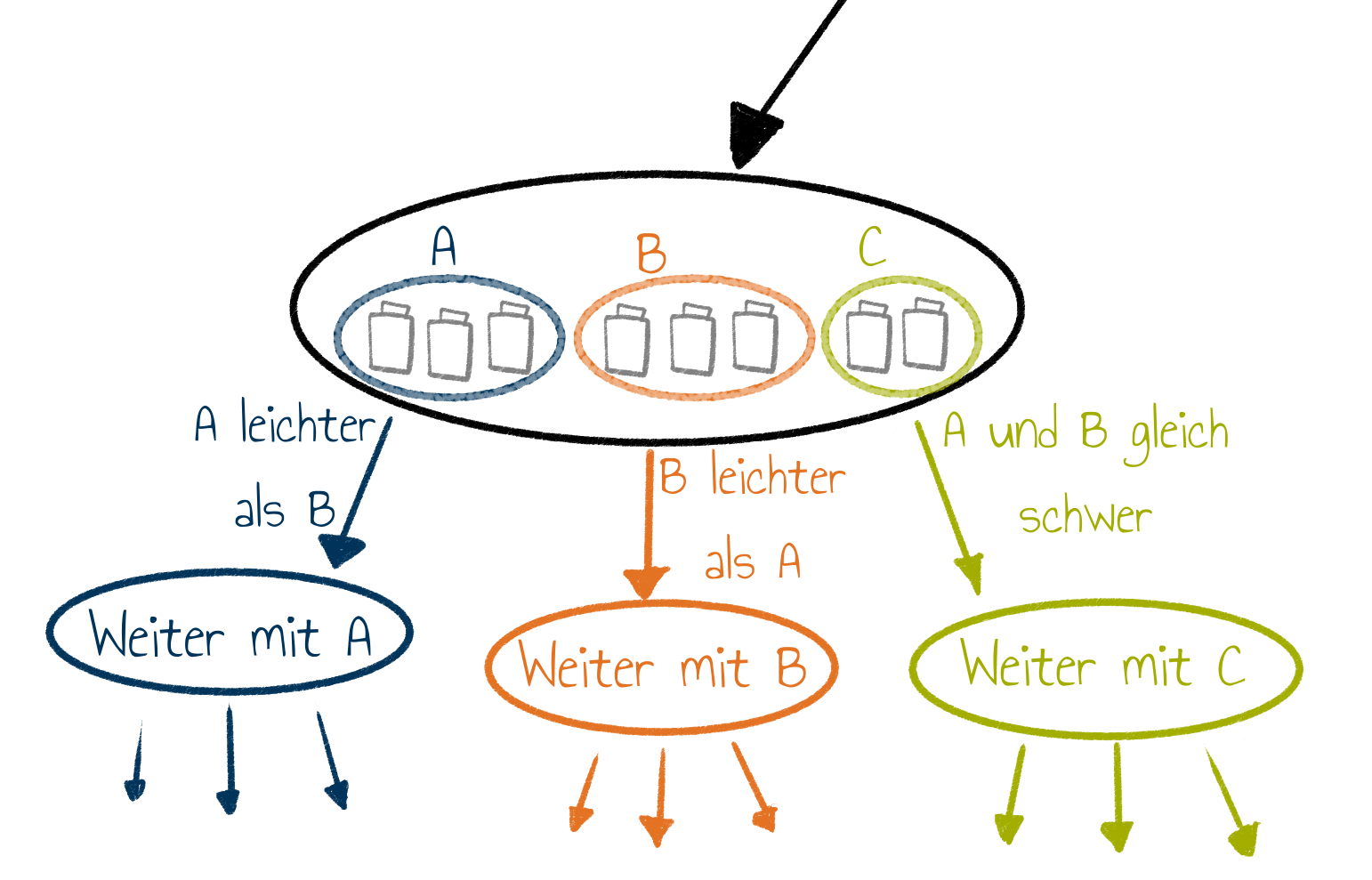
Damit ist der Entscheidungs-/Handlungsbaum, der diesen Ablauf beschreibt, ein Ternärbaum. Wie am Anfang der Seite beschrieben ist das ein Baum mit höchstens drei Kindern pro Knoten. Hierbei beschreibt jedes Kind eine der drei Teilmengen, auf die sich im weiteren Vorgehen beschränkt wird.

Es bleibt die Frage, wie die Mengen $A$, $B$ und $C$ am besten gewählt werden, damit dieser möglichst wenige Ebenen enthält. Denn jede neue Ebene beschreibt einen Wiegevorgang, welche minimiert werden sollen. Das Vorgehen hierbei ist nun analog zu den Überlegungen zur Gestaltung der Binärbaumsuche in einem Wörterbuch: Ohne zusätzliches Wissen darüber, wo das gesuchte Wort ist, sollte immer in der Mitte des Wörterbuchs begonnen werden. Die Menge der potenziellen Wörter wird folglich halbiert. Übertragen auf diese Situation bedeutet das, dass die Menge der Gewichte durch die Partitionierung gedrittelt werden sollte. Falls die Anzahl an Gewichten nicht durch 3 teilbar ist, sollten die Kardinalitäten der Teilmengen $A$, $B$ und $C$ so gleich wie möglich sein. Es ist nur notwendig, dass $A$ und $B$ gleich viele Gewichte enthalten – andernfalls ist es unnötig, sie gegeneinander zu wiegen.
Der Baum, der somit entsteht, hat in der $m$-ten Ebene $3^{m-1}$ Knoten und diese Ebene wird nach $m-1$ Wiegevorgängen erreicht. Die erste Ebene enthält nur die Wurzel und beschreibt die Ausgangsmenge aller $n$ Gewichte. Damit in einer solchen Ebene jeder Knoten genau ein übriggebliebenes Gewicht repräsentiert, muss $3^{m-1}\geq n$ sein. Aufgelöst ergibt sich $m-1\geq \log_3 n$. Das allgemeine Problem, dass am Anfang der Seite beschrieben wurde, lässt sich also folgendermaßen beantworten: Um aus $n$ Gewichten dasjenige zu finden, das leichter ist, reichen $\lceil\log_3 n \rceil$ Wiegevorgänge.
Wird das Ganze nun auf das ursprüngliche Problem mit acht Gewichten angewandt, sieht die Lösung wie folgt aus: Erst werden die Gewichte 1, 2 und 3 gegen 4, 5 und 6 gewogen. Ist eine der Mengen leichter, wird mit dieser fortgefahren. Sind sie gleich schwer, mit den Gewichten 7 und 8. In jedem Fall sind es jetzt nur noch drei oder zwei Gewichte, die zur Auswahl stehen. Sind es zwei (hier konkret Nummer 7 und 8), können sie einfach gegeneinander gewogen werden. Sind es drei, so werden zwei davon gewogen: Entweder 1 gegen 2 oder 4 gegen 5. Das gesuchte Gewicht ist entweder hier dabei und als leichteres auf der Waage zu sehen. Oder es ist das übriggebliebene (hier entweder 3 oder 6).