Euler-Touren

(Velminksi, 2008)

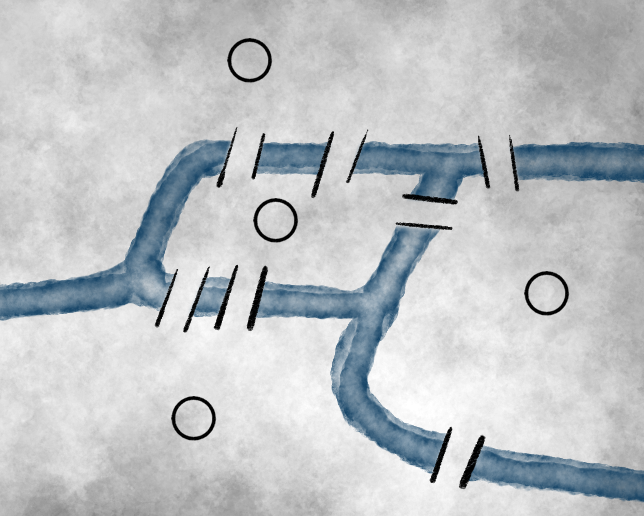
Im 18. Jahrhundert dachte Leonard Euler über folgendes Problem nach (Velminksi, 2008): Die Stadt Königsberg wird vom Pregel in vier Landgebiete bzw. Inseln unterteilt. Über den Pregel führen insgesamt sieben Brücken. Ist es möglich, an einem Punkt der Stadt einen Spaziergang zu beginnen, der genau einmal über jede Brücke führt und schließlich wieder am Ausgangspunkt endet?

Hier eine Skizze der Situation:

Um eine Lösung für dieses Problem zu finden, soll erst die gegebene Situation durch einen Graphen modelliert werden.

Die Standardinterpretation von Graphen sieht Knoten als Orte und Kanten als Verbindungen zwischen diesen. Hier ergibt es somit Sinn, die Stadtteile, die durch den Pregel getrennt sind, als Knoten zu nehmen und jede Brücke als Kante zwischen zwei Knoten.

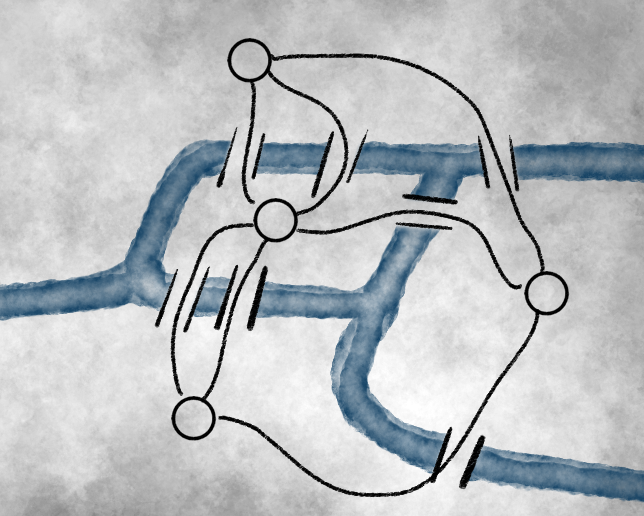
Ohne die Skizze der Stadt und mit etwas schöneren Kanten entsteht der folgende Graph:

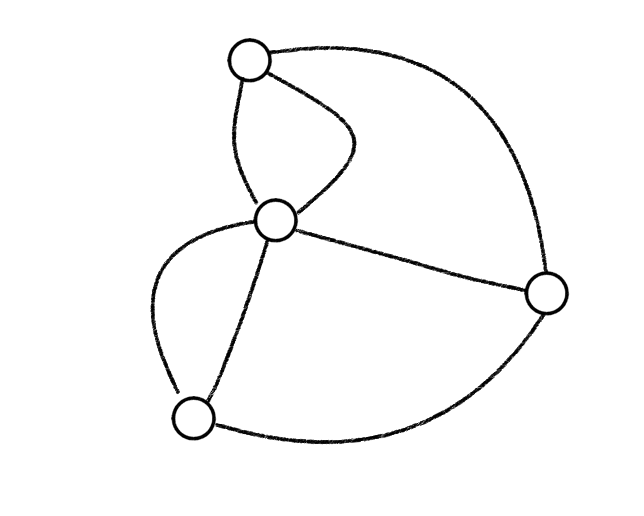
Zu sehen ist, dass es ein Multigraph ist; also ein Graph bei dem zwei Knoten durch mehrere Kanten miteinander verbunden sind. Wie auch immer die Lösung aussieht, sie muss beziehungsweise soll für beliebige Multigraphen funktionieren.

Der nächste Schritt besteht darin, das gegebene Problem in Termen eines Graphen zu beschreiben. Dazu wird die ursprüngliche Frage übersetzt: Gibt es einen Pfad in diesem Graph, sodass

1. alle Kanten genau einmal benutzt werden und
2. Start- und Endknoten identisch sind?

Ein derartiger Pfad wird Euler-Tour genannt. Die Frage nach der Existenz einer solchen Euler-Tour lässt sich ganz allgemein beantworten:

Satz: In einem zusammenhängenden Multigraph existiert genau dann eine Euler-Tour, wenn jeder Knoten geraden Grad hat. Dabei ist der Grad eines Knotens die Anzahl an Kanten, die an diesen Knoten anschließen.

Den Satz als Ganzes zu beweisen ist für den Schulunterricht nicht zu empfehlen. Die Implikation hingegen, dass in Graphen mit Euler-Touren alle Knoten geraden Grad haben müssen, ist für Lernende explorativ zugänglicher. Die Umkehrung – also, dass eine Euler-Tour existiert, wenn der Grad aller Knoten gerade ist – ist aufwendig und wird hier zum Abschluss nur der Vollständigkeit halber aufgeführt.

Beweis: Dass solch ein Rundlauf durch den gesamten Graphen nur dann möglich ist, wenn der Graph zusammenhängend ist, ist plausibel. Diese Bedingung sollte also mit vorausgesetzt werden. Es muss also noch geschlossen werden, dass in einem zusammenhängenden Graph mit Euler-Tour jeder Knoten geraden Grad hat, und umgekehrt.

Wenn eine Euler-Tour existiert und man über eine Kante in einen Knoten hineinläuft, muss man über eine andere Kante hinauslaufen. Denn jede Kante soll verwendet werden. Jedes Mal, wenn dieser Knoten besucht wird, werden zwei seiner Kanten für die Euler-Tour “aufgebraucht”. Es muss also insgesamt immer eine Anzahl an Kanten an einen Knoten anschließen, die ein Vielfaches von zwei ist. Nur beim Start-/Endknoten sieht das ein bisschen anders aus: Dort läuft der Pfad am Anfang hinaus und erst ganz am Ende wieder hinein. Das verwendet genau zwei Kanten. Wird er zwischendurch erreicht, greift dasselbe Argument wie für alle anderen Knoten.

Um die Umkehrung zu beweisen, nehmen wir an, dass wir einen zusammenhängenden Graph haben, indem jeder Knoten geraden Grad hat. Sei $W$ der längste Pfad in diesem Graphen, der jede Kante höchstens einmal verwendet, und seien die Knoten, die durch ihn abgelaufen werden,

\[v_0, v_1, …, v_k.\]

Hier ist zu beachten, dass Knoten $v_i$ und $v_j$ an verschiedenen Stellen $i$ und $j$ gleich sein können. Es müssen alle Kanten, die an $v_k$ anschließen, in diesem Pfad enthalten sein. Denn sonst könnte er um solch eine nicht-verwendete Kante erweitert werden. Nun bleibt die Behauptung, dass dieser Pfad $W$, der immer existiert, eine Euler-Tour ist. Als Erstes gilt, dass $v_k = v_0$ ist: Andernfalls wäre $W$ einmal mehr in $v_k$ hinein- als herausgelaufen und $v_k$ hätte ungeraden Grad. Also muss $v_k$ in diesem Pfad mehrfach auftauchen. Außerdem werden alle “inneren” Knoten von $W$ immer in Vielfachen von 2 verwendet und somit ist $v_0$ der einzige Knoten, an den die Kante $v_{k-1} v_k$ anschließen kann. Als Zweites gilt, dass $W$ wirklich alle Kanten enthält: Würde er das nicht tun, existiert mindestens eine Kante, die nicht in $W$ enthalten ist, aber an einen Knoten im Pfad anschließt. Denn der Graph ist zusammenhängend. Nennen wir diese Kante $u v_i$, wobei $v_i$ in $W$ liegt. Nun kann daraus ein weiterer Pfad konstruiert werden, der länger als $W$ ist und trotzdem jede Kante höchsten einmal verwendet. Dieser neue Pfad ist konkret durch die Knotenfolge

\[u, v_i, v_{i+1},…,v_k, v_1,v_2,…,v_i\]

gegeben. Das widerspräche jedoch der Definition von $W$ und somit muss $W$ bereits alle Kanten im Graph enthalten.