Weiterführende Themen
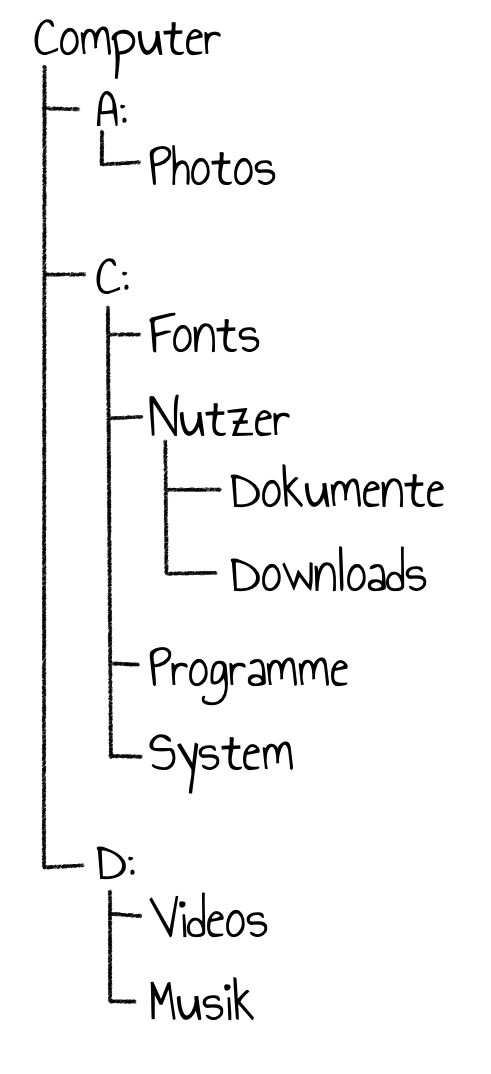
Binärbäume finden in der Informatik mehr Anwendungen als nur als Mittel zur effizienten Suche in sortierten Datenmengen. Zum Beispiel werden sie als Hash-Bäume verwendet: Diese erlauben es, Daten auf Integrität zu überprüfen; ähnlich wie die Prüfsumme am Ende einer ISBN. Außerdem sind alle Orderstrukturen und Dateisysteme in Computer mittels Bäumen modelliert/implementiert.
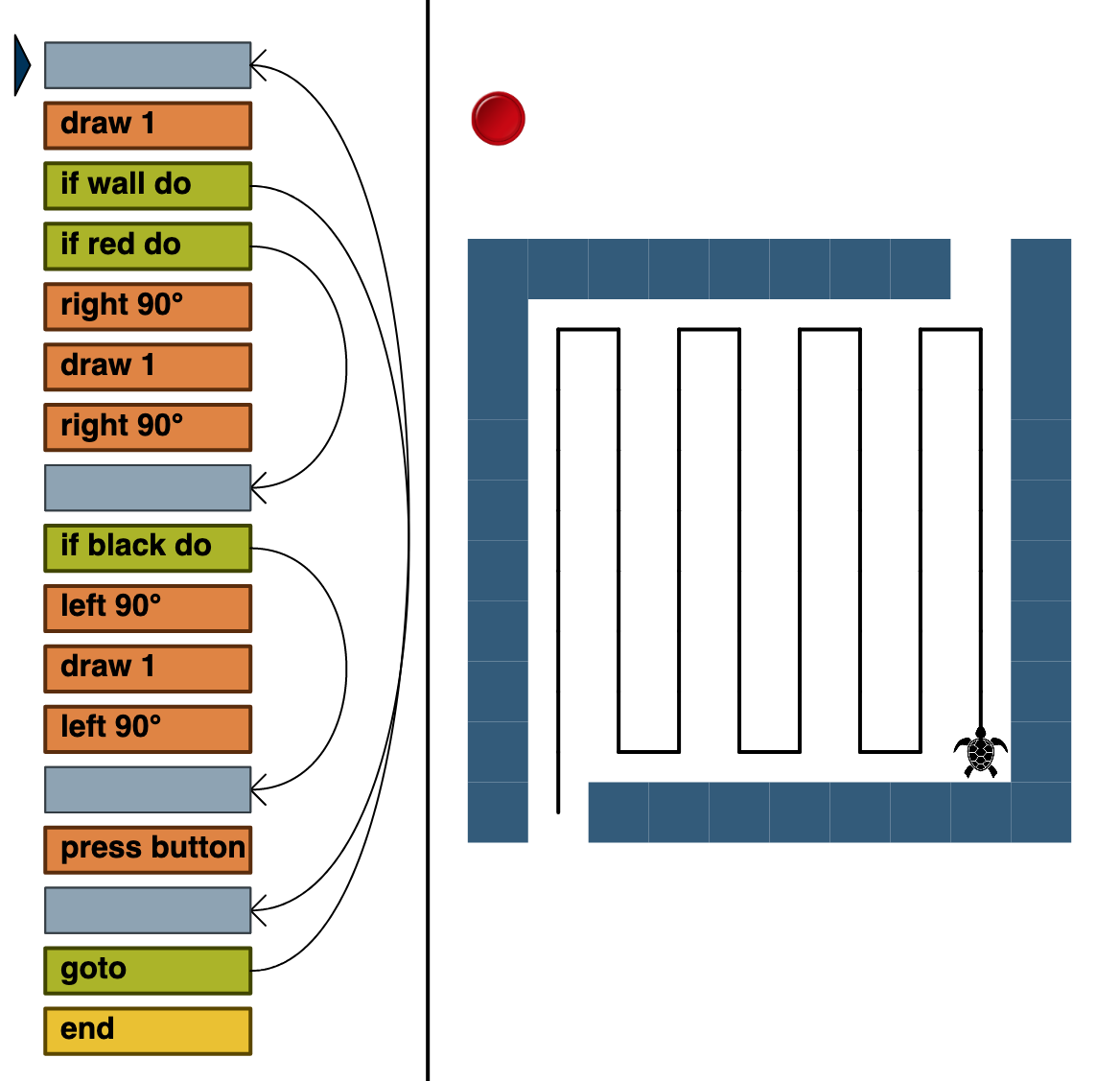
Auch als Werkzeug zur Darstellung und Bearbeitung von Computercode finden Graphen Verwendung, was schon bei deren Einführung hier angedeutet wurde. Wie im Modul Heterogenität und adaptiver Unterricht – Rolle von Fehlern – Algorithmik dargelegt, ist es sehr aufwendig, die allgemeine Logik und Semantik von Algorithmen und Programmen parallel zur Syntax einer Programmiersprache zu lernen. Darum wird für theoretische Überlegungen Pseudocode verwendet. Für eine praktische Umsetzung ist dieser jedoch ungeeignet, da ihm zu viel Struktur fehlt. Aushilfe schafft graphische Programmierung: Zum Beispiel wurde im oben erwähnten Modul eine Programmierumgebung eingeführt, in der eine Schildkröte gesteuert werden soll. Dazu werden relativ einfache Anweisungen verkettet. In dieser Sequenz kann allerdings auch außer Reihe nach oben oder unten gesprungen werden. Diese Assembler-ähnliche Sprache wird dadurch verständlich, dass Pfeile den Verlauf zwischen den Befehlen angeben. Damit stellen sie gerichtete Kanten und Knoten in einem Graphen dar.
Elaboriertere Varianten derselben Idee können in modernen Softwareentwicklungsumgebungen wie Unreal Engine, Unity oder Godot gefunden werden. Dort erlauben es Graphen komplexe Programme zu erstellen, komplett ohne die Syntax der zugrunde liegenden Programmiersprache zu kennen.
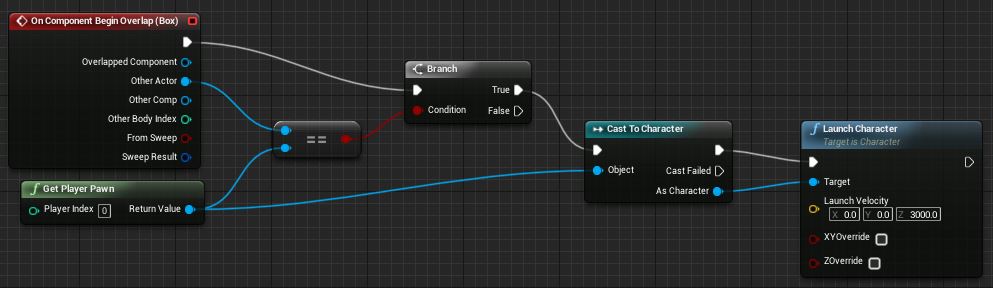Abbildung: Beispiel eines Unreal Engine 4 Blueprints von Epic Games, https://docs.unrealengine.com/en-US/Engine/Blueprints/QuickStart/index.html
In der Mathematik werden Graphen hauptsächlich dafür benutzt, komplizierte Sachverhalte so zu modellieren, dass sie einfacher analysiert werden können: Auf diese Art und Weise bewies z. B. Hao Huang (2019) die ‘Sensitivity’-Vermutung – eine Aussage aus der theoretischen Informatik, welche insbesondere die Struktur von Schaltkreisen beschreibt und welche 30 Jahren bestand, bevor sie bestätigt wurde. Das Besondere an dem Beweis von Huang ist, dass er außergewöhnlich kurz ausfällt. (Der Beweis selbst findet auf zwei Seiten Platz; das zugehörige Paper umfasst sechs Seiten.) Huang gelang es, die abstrakte Aussage so umzuformulieren, dass sie durch einen speziellen Graphen beschrieben werden konnte: dem Graph, welcher die Ecken und Kanten eines Hyperwürfels (einem verallgemeinertem Würfel in Dimensionen höher als 3) beschreibt. Und die übersetzte Aussage konnte dann von Huang durch relativ einfache geometrische Überlegungen bewiesen werden.
Wie hier im Modul selbst und im zugehörigen Unterrichtsvideo zu sehen ist, können Graphen als allgemeine Netzwerke eingeführt werden. Ist im Schulunterricht genug Zeit, lohnt es sich, mit den Schülerinnen und Schülern etwas über den Tellerrand von Straßenplänen und Wörterbuchsuchen hinauszublicken. Die Beispiele, die auf dieser Seite beschrieben wurden, sind für den Schulunterricht aber in aller Regel zu kompliziert und zu aufwendig ist – oder wie im Falle der Ordern in einem Computersystem nicht interessant genug. Deswegen werden im Anschluss nun noch drei Bespiele betrachtet werden, die für Schülerinnen und Schüler leichter zu erarbeiten und zu verstehen sind. Dazu werden auch andere Arten von Graphen verwendet als Bäume, um noch einmal hervorzuheben, wie die Graphentheorie allgemein zur Modellierung und Lösung von Problemen genutzt werden kann.