Via Rekursion

Die Implementierung als Array funktioniert so lange gut, wie der Baum sich nicht ändert. Beschreibt dieser dynamische Listen, so sollte er auch flexibel agieren können. Das kann dadurch ermöglicht werden, dass Bäume selbst-ähnliche Strukturen sind: Die Teilgraphen, die an der Wurzel hängen, sind selbst wieder Bäume. Insbesondere sind die Nachbarknoten der Wurzel eine natürliche Wahl für Wurzeln dieser Teilbäume.

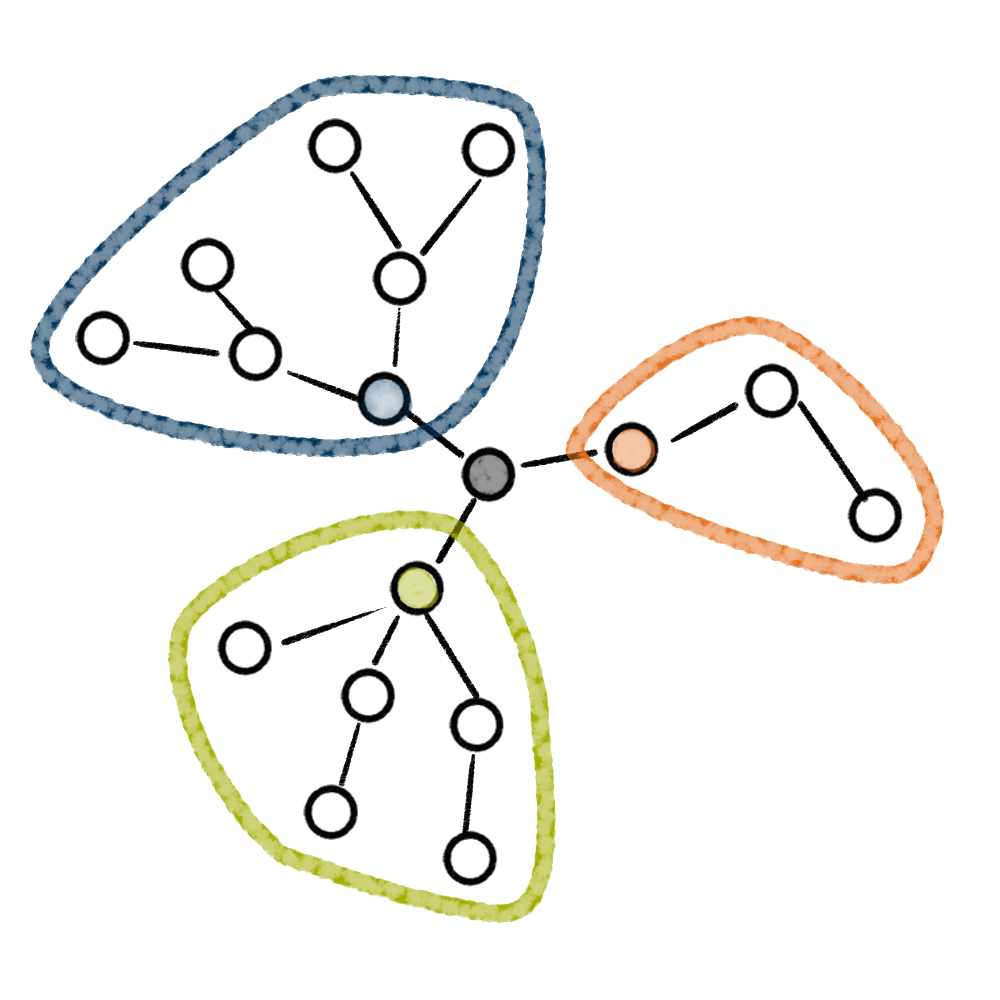
Das erlaubt einen Baum als rekursive Datenstruktur umzusetzen: Ein Baum b ist vollständig und eindeutig durch die Festlegung einer Wurzel w(b) und allen Bäumen k1(l), …, kn(l) die an w(b) hängen, bestimmt. Die kleinsten Einheiten sind dabei die Blätter: als Bäume, die nur aus der Wurzel bestehen. Für Binärbäume im Speziellen heißt das, dass sie durch die Wurzel w(b) und deren linken Kindbaum l(b) und rechten Kindbaum r(b) bestimmt sind.

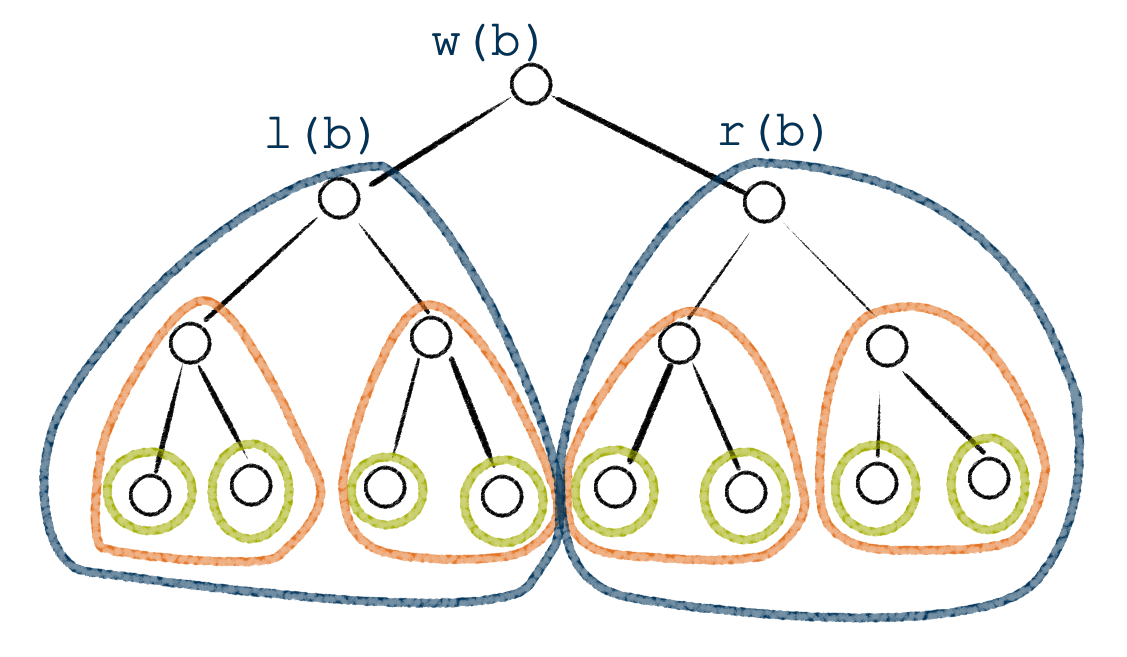
In dieser Form stellen (Binär-)Bäume ein für die Praxis wichtiges Beispiel der objektorientierten Programmierung dar, welches speziell die Konzepte der Abstraktion und Datenkapselung veranschaulicht. Somit eignen sich Bäume als Anwendungsbeispiel in diesem Themenkomplex.

Die Implementierung der Binärbaumsuche selbst wird durch diese Architektur vereinfacht. Insbesondere ist die genaue Gestalt des Baums nicht mehr wichtig – im Gegensatz zur Implementierung als Array. So kann mit folgender Suchanfrage auch ein allgemeinerer Binärbaum durchsucht werden, wie er in Aufgabe 10 zu diesem Modul zu sehen ist. Der folgende Pseudocode zeigt die grundlegende Struktur der Binärbaumsuche, wenn die Binärbäume wie eben beschrieben rekursiv implementiert sind:

suche(Eintrag e, Baum b) {
    Ist e == w(b)? Falls ja:
        Gib e aus.
    sonst:
        Ist e < w(b)? Falls ja:
            suche(e, l(b))
        sonst:
            suche(e, r(b))
}