Als Array
Zum Abschluss sollen noch einige Informationen dazu vorgestellt werden, wie ein Baum tatsächlich implementiert werden kann.
In einem Computersystem werden die Datenfolgen oft als Arrays gespeichert – also als Liste fester Länge. Die Speicherbits auf der Platine sind der Reihe nach sortiert, da der Computer immer genau wissen muss, an welcher Stelle welche Information gespeichert ist. Und für Arrays werden hintereinander liegende Bits verwendet. Darum bietet es sich oft an, einfache Datenstrukturen auch als Array zu speichern – aber so, dass die Struktur leicht wiederherzustellen und zu benutzen ist. Und bei Binärbäumen ist das ganz besonders einfach:
Die Einträge in einem Binärbaum werden erst Ebene für Ebene sortiert und anschließend jeweils von links nach rechts. Dann ist das linke Kind des $i$-ten Knoten der $(2i)$-te Knoten und sein rechtes Kind der $(2i + 1)$-te Knoten. Umgekehrt ist sein Elternknoten der $\left\lfloor\frac{i}{2}\right\rfloor$-te Knoten. Das macht es also sehr einfach, in einem Computerprogramm durch einen Binärbaum zu laufen, ohne Kinder und Elternknoten extra speichern zu müssen. Das nachfolgende Beispiel verdeutlicht dies:
Wie im vorhergehenden Abschnitt bereits erklärt, kann die Liste ‘age’, …, ‘year’ durch den folgenden Baum dargestellt werden.
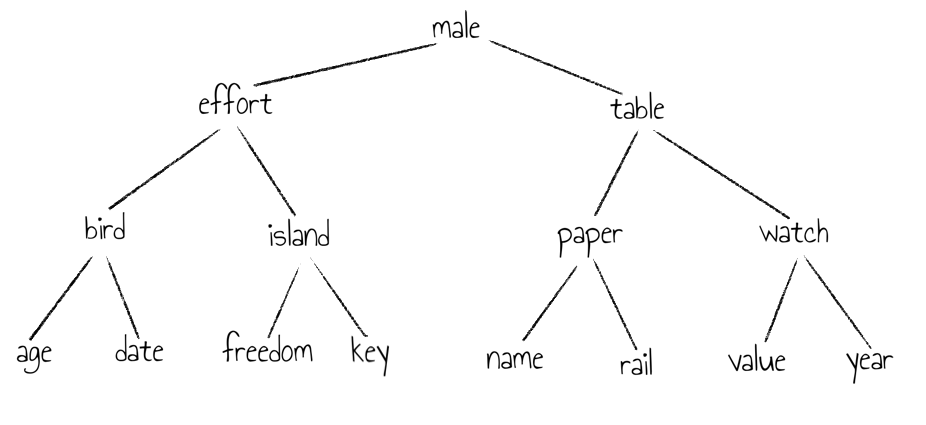
Und wird das Wort ‘island’ gesucht, sieht das folgendermaßen aus:
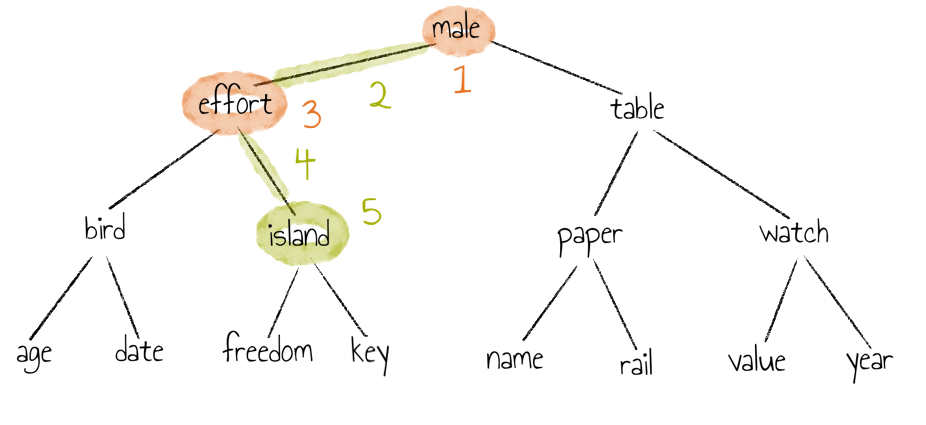
Um diesem Baum nun als Array zu implementieren, werden die Knoten zeilenweise sortiert:
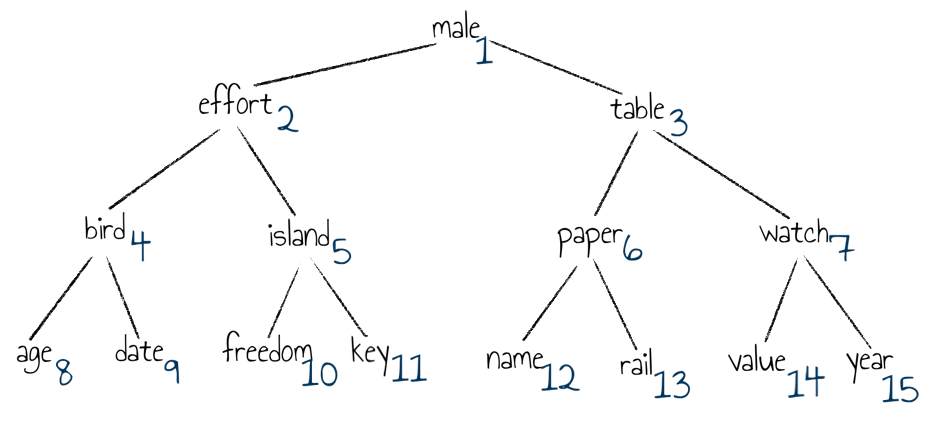
Das Element, das in der Mitte der Liste steht, ist also das erste. Anschließend kommen die mittleren Elemente der vorderen und hinteren Teillisten, usw. Damit ergibt sich das folgende Array als diejenige Datenstruktur, die in der Praxis dann tatsächlich genutzt wird.
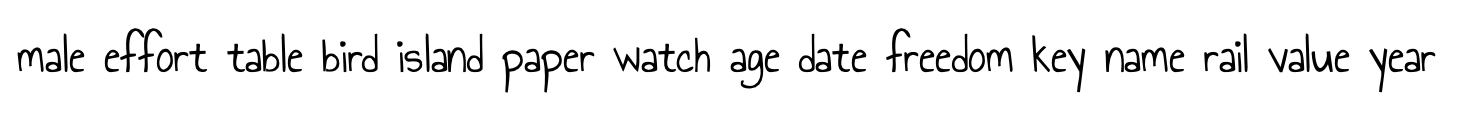
Die Baumstruktur, die dann alleine durch die Indizes – also der Stelle im Array – gegeben ist, sieht so aus:
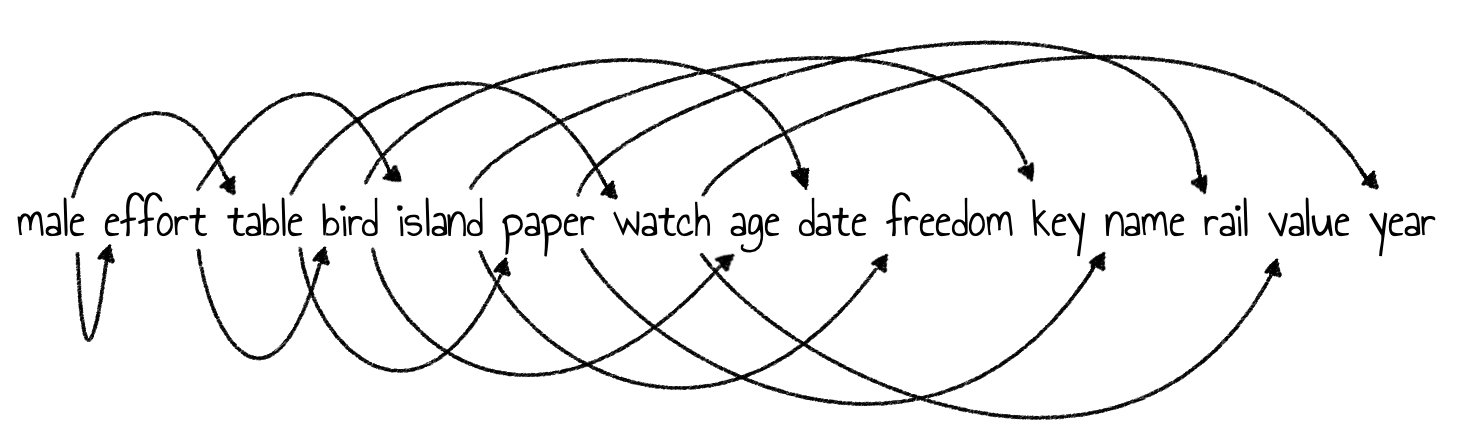
Wie oben bereits beschrieben, entspricht der Übergang $i\leadsto 2i$ der Kante zum linken Kind und $i\leadsto 2i + 1$ der Kante zum rechten Kind. Wird also der Eintrag ‘island’ gesucht, so springt der Algorithmus von Eintrag $i = 1$ zu Eintrag Nummer $2i = 2$ und anschließend von $i= 2 $ zu Eintrag Nummer $2i + 1 = 5$.
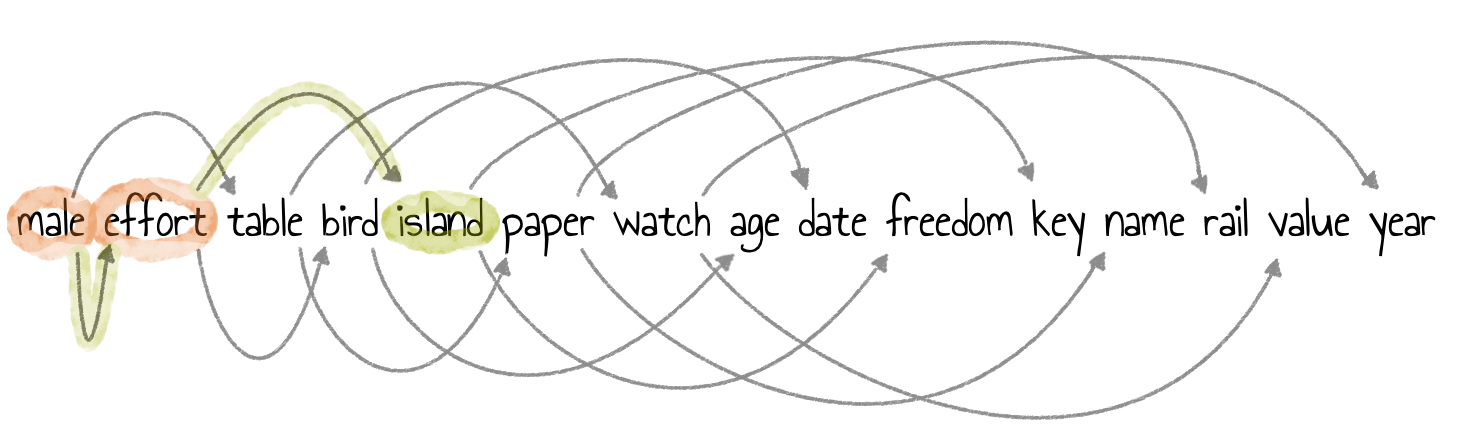
Weiterführende Informationen zu Bäumen als Datenstrukturen finden Sie in (Dietzfelbinger, Mehlhorn, & Sanders, 2014).