Rechtwinklige Dreiecke mit Hypotenuse gleich 1

Als zweiten Spezialfall betrachten wir rechtwinklige Dreiecke mit einer Länge der Hypotenuse gleich 1. 

Es ist bekannt, dass für Sinus & Cosinus folgender Zusammenhang gilt:

• $\displaystyle\sin(\alpha )=\frac{\text{Gegenkathete}}{\text{Hypotenuse}} $
• $\displaystyle\cos(\alpha )=\frac{\text{Ankathete}}{\text{Hypotenuse}} $

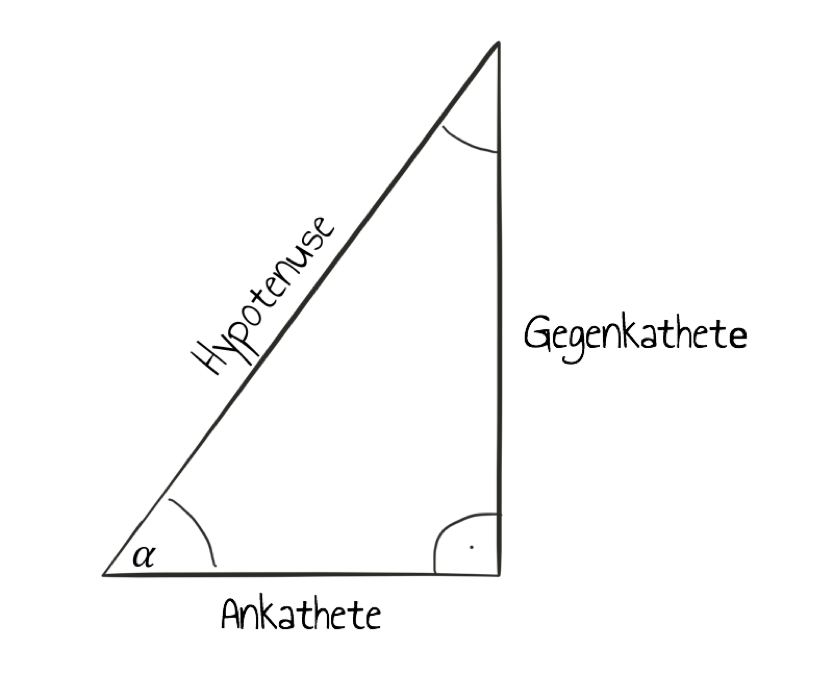
Da die Länge der Hypotenuse gleich 1 ist, ergeben sich die beiden Katheten direkt:

• $\sin(\alpha )=\text{Gegenkathete}$
• $\cos(\alpha )=\text{Ankathete}$

Weiterhin kann der Satz des Pythagoras angewandt werden, um einen weiteren Zusammenhang zwischen Sinus und Cosinus zu erhalten. 

\[c^2=a^2+b^2 \Leftrightarrow\]

\[1^2=\sin^2(\alpha )+\cos^2(\alpha)\]

Diese Gleichung wird auch als trigonometrischer Pythagoras bezeichnet. Dieser kann geometrisch am Einheitskreis wie folgt veranschaulicht werden:

Anleitung: Den Schieberegler unterhalb des Koordinatensystems von links nach rechts bewegen.