Multigraphen, Schleifen & gerichtete Graphen
Graphen tauchen in Theorie und Praxis in vielen Spezialformen auf. Die wichtigsten sind:
- Multigraphen: Wenn es zwischen zwei Knoten mehrere Kanten gibt.
- Schleifen: Wenn es Kanten gibt, die einen Knoten mit sich selbst verbinden.
- Gerichtete Graphen: Ob die Beziehung zwischen den Knoten asymmetrisch ist, oder nicht.
Der erste Fall taucht zum Beispiel bei U-Bahnplänen auf. Sind die Haltestellen die Knoten und die U-Bahnlinien die Kanten, so können durchaus zwei Haltestellen durch mehrere Linien verbunden sein.
Der zweite Fall wird beim Beispiel zur Teilbarkeit von natürlichen Zahlen im vorhergehenden Abschnitt relevant. Dort wurden zwei verschiedene Zahlen verbunden, wenn eine die andere teilt. Aber natürlich teilt jede Zahl sich selbst und deswegen müsste dort jeder Knoten mit sich selbst verbunden sein.
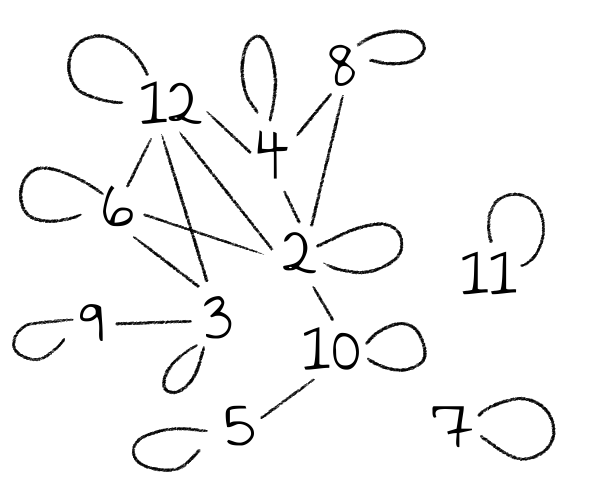
Ob das sinnvoll ist, hängt dann davon ab, welche Art von Modellierung, Berechnung oder Analyse mit so einem Graphen im Anschluss gemacht werden soll.
Der letzte Spezialfall gerichteter Graphen modelliert asymmetrische Beziehungen wie z. B. Einbahnstraßen: Kann in einem Straßennetz nur von einem Ort direkt zum anderen gelaufen werden, aber nicht zurück, so bietet es sich an, diese Beziehung durch einen gerichteten Graphen darzustellen. Dort sind die Kanten dann keine Linien mehr, sondern Pfeile, die die Von-Nach-Beziehung visualisieren.
Ein anderes Beispiel für gerichtete Graphen ist, erneut, der Teilbarkeitsgraph. Wenn zwei verschiedene natürliche Zahlen $a$ und $b$ dort miteinander verbunden sind, so wird $a$ von $b$ geteilt oder $b$ von $a$. Da die Zahlen aber verschieden sind, kann nur einer von beiden Fällen eintreten. Somit ist es sinnvoll, in diesem Graphen gerichtete Kanten zu verwenden, die von der kleineren zur größeren Zahl zeigen.
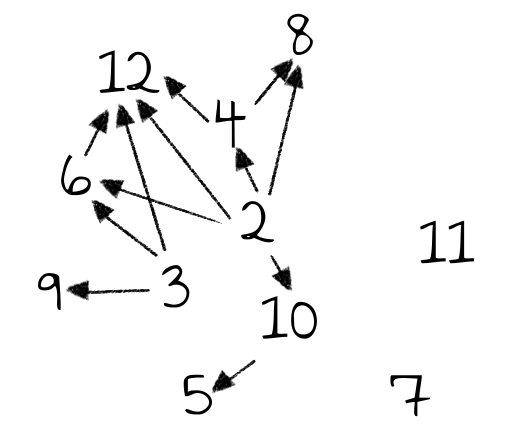
Weiterführende Informationen zur Einführung von Graphen finden Sie in (Aigner, 2015).