Beweisen nach dem Vorbild von Experten/innen
(Boero, 1999; Brunner, 2014; Reiss & Ufer, 2009)
Beweisen lernen und lehren nach dem Vorbild von Experten
Um den Prozess des mathematischen Beweisens besser verstehen zu können, hat sich Boero (1999) das explizite Vorgehen von Experten genau angeschaut.
Er hat festgestellt, dass die Experten während des Beweisprozesses sechs verschiedene Phasen durchlaufen. Die einzelnen Phasen spiegeln die Fähigkeiten wieder, die zu einer Beweisführung nötig sind.
Reiss & Ufer (2009, S.162) haben eine siebte Phase hinzugefügt, die sich konkret auf die Schule bezieht. Diese sieben Phasen, die in der unteren Graphik aufgezählt sind, können eine Orientierung für das Argumentieren, Begründen und Beweisen im Mathematikunterricht darstellen und als Bearbeitungshilfen eingesetzt werden.
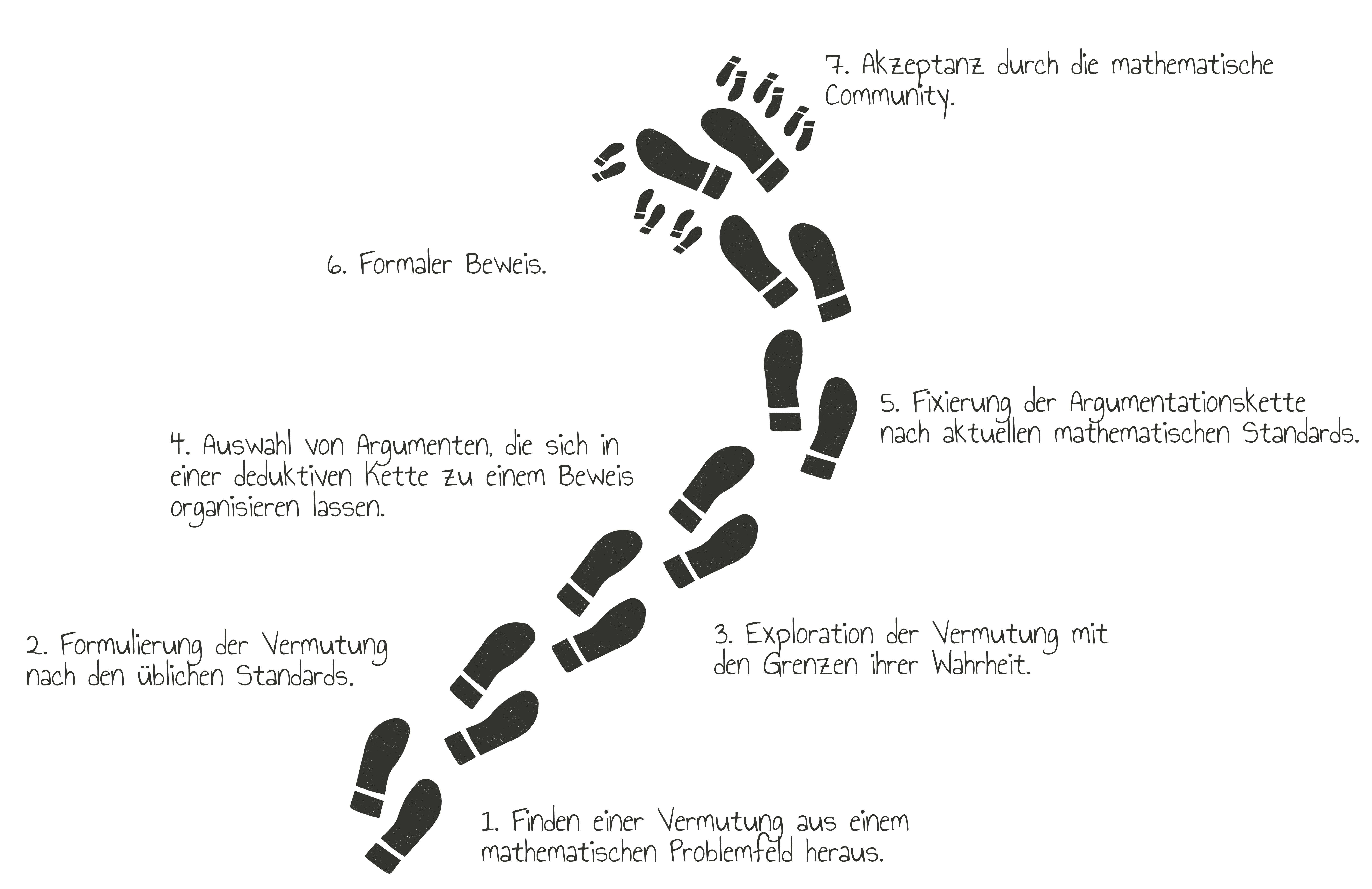
Brunner (2014, S.61-62) kritisiert, dass Boeros Modell kein zirkuläres Element besitzt und damit keinen Raum für das Lernen aus Fehlern nach Wiederholungen und Neuanfängen zulässt. Außerdem vermisst sie ein genetisches Verständnis, das bei der Entwicklung des Beweises nach Boeros Phasen nicht eingearbeitet ist.
Anwendung des Modells auf den Zerlegungsbeweis
Betrachten Sie erneut den Beweis, der auf dem Prinzip der Zerlegungsgleichheit beruht. Er ist sicher einer der komplexeren Beweise, jedoch können wir an ihm die einzelnen Phasen des Modells gut erkennen.
Phase 1: Finden einer Vermutung aus einem mathematischen Problemfeld heraus
Vermutung: Zwei Figuren sind zerlegungsgleich, wenn man die eine so zerschneiden kann, dass man aus den entstehenden Puzzleteilen die andere zusammensetzen kann.
Phase 2: Formulierung der Vermutung nach den üblichen Standards
Auf unser Problem angewandt, bedeutet das, dass der Satz des Pythagoras bewiesen ist, wenn wir die Kathetenquadrate und das Hypothenusenquadrat derart zerlegen können, dass gleiche Teilfiguren entstehen.
Phase 3: Exploration der Vermutung mit den Grenzen ihrer Wahrheit
Mit der dynamischen mathematischen Visualisierung können wir Vermutungen aufstellen, ob dies immer gilt oder ob es bestimmte Spezialfälle gibt, in denen diese Zerlegung nicht mehr funktionieren würde.
Phase 4: Auswahl von Argumenten
Im Beweis sehen Sie ab dem Punkt “Beweis der Behauptung”, wie verschiedene Eigenschaften gesammelt werden, die später für den Beweis gebraucht werden.
Phase 5: Fixierung der Argumentationskette
Dies können wir in den zwei Schritten gegen Ende des Beweises nachvollziehen.
Phase 6: Formaler Beweis
Wir müssten nun nur noch unsere Überlegungen arithmetisch ausführen, dann wäre der formale Beweis getan.
Phase 7: Akzeptanz durch die mathematische Community
Durch eine Internetrecherche könnte herausgefunden werden, wie damals auf den Beweis von Henry Perigal reagiert wurde. Wird der Beweis in der Klasse nachvollzogen, könnte eine Diskussion im Plenum diesen Schritt erfüllen.