Unterschied zwischen Listen und Bäumen

Solche Bäume sollen nun als Datenstruktur verwendet werden. Sprich, die Knoten stellen keine Operationen und allgemeine Anweisungen dar, sondern konkrete Daten, die abgerufen werden sollen.

Aus dem Informatikunterricht sind zu diesem Zeitpunkt Listen bereits als Struktur zur Datenspeicherung bekannt. Diese sind dadurch gekennzeichnet, dass sie einen Starteintrag haben und dass jeder Eintrag bis auf den letzten einen Nachfolger besitzt. Damit sind sie Spezialfälle von Bäumen.

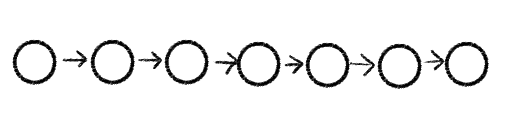
Das Problem mit Listen ist, dass es im Allgemeinen sehr lange dauern kann, einen Eintrag zu finden. Soll z. B. ein Wörterbuch nach einem Eintrag durchsucht werden, so muss mit einem naiven Ansatz von vorne durchgegangen und jeder einzelne Eintrag überprüft werden. Ist der Eintrag an Stelle Nummer 34262345, werden auch 34262345 einzelne Überprüfungsschritte gebraucht, um ihn zu finden.

Ist eine große Menge geordneter Daten gegeben, in der etwas gesucht werden soll, so bieten sich Binärbäume an. Das sind Bäume, in denen jeder Knoten, der kein Blatt ist, genau zwei Kinder hat. Wie in nachfolgender Szene 4: Einführung von Binärbäumen zu sehen ist, kann solch ein Binärbaum als Abfolge von Ja-Nein-Fragen angesehen werden. Jede dieser Fragen teilt die Menge an Kandidaten in zwei Hälften. Das bedeutet, dass nach fünf Fragen nur noch $\frac{1}{2^5} = \frac{1}{32}$ aller Objekte übrig ist und nach zehn Fragen sogar nur $\frac{1}{2^{10}} = \frac{1}{1024}$. Dieses exponentiell-schnelle Ausschließen erlaubt, dass auch große Datenmengen schnell durchsucht werden können.

Szene 4: Einführung von Binärbäumen zeigt ebenfalls, dass bessere/effektivere Fragen gestellt werden können, wenn zusätzliche Informationen über ein vorliegendes Problem vorhanden sind.

Ist die Datenmenge ungeordnet, muss allerdings jedes einzelne Element überprüft werden, bis das gewünschte gefunden wurde.

Weiterführende Informationen zu Bäumen als Datenstrukturen finden Sie in (Dietzfelbinger, Mehlhorn, & Sanders, 2014).